
"One of the most useful principles of enumeration in discrete probability and combinatorial theory is the celebrated principle of inclusion–exclusion. If M and N are any two topological spaces, then the Euler characteristic of their disjoint union is the sum of their Euler characteristics, since homology is additive under disjoint union: + (). This inverse has a special structure, making the principle an extremely valuable technique in combinatorics and related areas of mathematics. In a very abstract setting, the principle of inclusion–exclusion can be expressed as the calculation of the inverse of a certain matrix. More generally, both versions of the principle can be put under the common umbrella of measure theory.

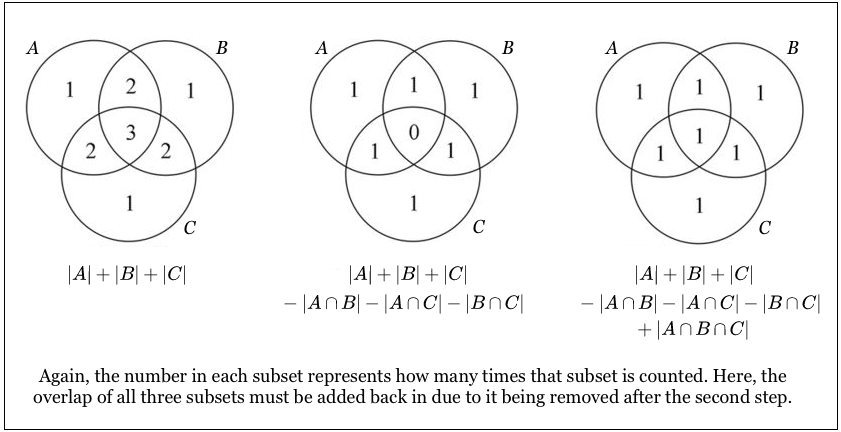
Īs finite probabilities are computed as counts relative to the cardinality of the probability space, the formulas for the principle of inclusion–exclusion remain valid when the cardinalities of the sets are replaced by finite probabilities. The principle can be viewed as an example of the sieve method extensively used in number theory and is sometimes referred to as the sieve formula. Sometimes the principle is referred to as the formula of Da Silva or Sylvester, due to these publications. This concept is attributed to Abraham de Moivre (1718), although it first appears in a paper of Daniel da Silva (1854) and later in a paper by J. The name comes from the idea that the principle is based on over-generous inclusion, followed by compensating exclusion. Continue, until the cardinality of the n-tuple-wise intersection is included (if n is odd) or excluded ( n even).Include the cardinalities of the quintuple-wise intersections.Exclude the cardinalities of the quadruple-wise intersections.Include the cardinalities of the triple-wise intersections. The inclusion-exclusion principle enables us to count the natural numbers between 1 and n (inclusive) which are not coprime to n in two ways.Exclude the cardinalities of the pairwise intersections.To find the cardinality of the union of n sets: Generalizing the results of these examples gives the principle of inclusion–exclusion. Inclusion–exclusion illustrated by a Venn diagram for three sets In this case, when removing the contributions of over-counted elements, the number of elements in the mutual intersection of the three sets has been subtracted too often, so must be added back in to get the correct total. This formula can be verified by counting how many times each region in the Venn diagram figure is included in the right-hand side of the formula. The inclusion-exclusion principle, being a generalization of the two-set case, is perhaps more clearly seen in the case of three sets, which for the sets A, B and C is given by | A ∪ B ∪ C | = | A | + | B | + | C | − | A ∩ B | − | A ∩ C | − | B ∩ C | + | A ∩ B ∩ C | The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection. Suppose we have a set X with subsets A and B. To form such a study group, we just need to choose at least 2 of the remaining 17. The inclusion-exclusion principle, is among the most basic techniques of combinatorics. Instead of counting study groups that include at least one of Alicia, Bob, and Sue, we will count study groups that don’t include any of Alicia, Bob, or Sue. The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. By the principle of inclusion-exclusion, jABSj 3 (219 1) 3 218 + 217. For example if we want to count number of numbers in first 100 natural numbers which are either divisible by 5 or by 7. Where A and B are two finite sets and | S | indicates the cardinality of a set S (which may be considered as the number of elements of the set, if the set is finite). The principle of inclusion and exclusion is a counting technique in which the elements satisfy at least one of the different properties while counting elements satisfying more than one property are counted exactly once. Note there is just 0! = 1 permutation of the empty set.Counting technique in combinatorics Venn diagram showing the union of sets A and B as everything not in white This is essentially a proof by induction, where the empty sequence comprising the set S 0 can be chosen in just one way. To construct a sequence of S a, we may choose the first element in a ways, and then the remaining sequence of a − 1 elements may be chosen in (a − 1)! ways, yielding a! ways overall. (In general, we write #S to denote the number of elements in the set S, thus for example, #N a = a.) The symbol ! is called the factorial operator.
We have #S a = a! where a! := a(a − 1)(a − 2) Note we sometimes, as in this example, write sequences without commas separating the sequence elements.


 0 kommentar(er)
0 kommentar(er)
